FDR promotes confounds

Exploring a problematic aspect of false discovery rate correction in fMRI

December 10, 2020 by Mark

Everyone with experience conducting fMRI research knows about the problem of multiple comparisons. Simply put, the more statistical tests you run, the greater the chance that at least one of them produces a false positive. When one simultaneously tests every one of the hundreds of thousands of voxels in a brain image, one is almost certain to see numerous false positives. For this reason, all modern fMRI studies that test voxelwise effects must somehow correct for multiple comparisons.

Most corrections for multiple comparisons attempt to control the family-wise error (FWE) rate. That is, they try to limit the expected probability of any false positive to .05. There are many ways to achieve FWE control, and much ink has been spilled over their various features and flaws. However, many papers eschew FWE altogether in favor of a different standard: FDR, or false discovery rate. Rather than controlling the probability of any false positive, FDR attempts to limit the proportion of positives that are false. With the typical q = .05, this mean that you should expect that 5% of the "significant" voxels you see in an FDR-corrected image are, in fact, false positives.

Since FDR permits false positives, it should be clear that it is a more liberal standard than FWE. This is arguably a virtue of FDR: given that any fMRI studies are likely underpowered, a more lenient standard may help more appropriately balance the risks of false positives and false negatives. However, the liberality of FDR is actually variable. When there are no significant voxels in the brain, FDR is just as conservative as FWE. However, as more and more significant voxels appear in an image, the FDR becomes increasingly liberal. This adaptability is often marketed as a feature, but it is the crux of the problem I will consider here.

The claim I advance is that FDR's adaptability promotes confounded fMRI experiments. The reasoning is as follows: FDR becomes increasingly liberal as a function of the number of significant voxels anywher in the brain. Large numbers of significant voxels can be produced via a confounded experimental manipulation or individual difference measure. For example, if one is studying a social cognitive effect, but does not bother to control for incidental visual differences between stimuli in different conditions, one's manipulation is liable to produce a large significant activation in visual cortex. If the results are corrected via FDR, the visual cortex activation will consequently lower the standard for significance across the brain, increasing one's odds of observing a significant result in other regions. Given the strong publication bias favoring significant vs. null results, using confounded designs thus actually improves one's odds of publishing, if using FDR.

Simulations

The line of reasoning above may not be immediately convincing if you haven't spent a lot of time thinking about this issue already. Therefore, I've run a very simple Monte Carlo simulation to provide proof of concept for this argument. These simulations don't reflect every aspect of real fMRI data, since assembling a realistic simulation would be a much more time-consuming prospect. However, I do not believe that any of the overlooked nuances undermine the main point of my claim.

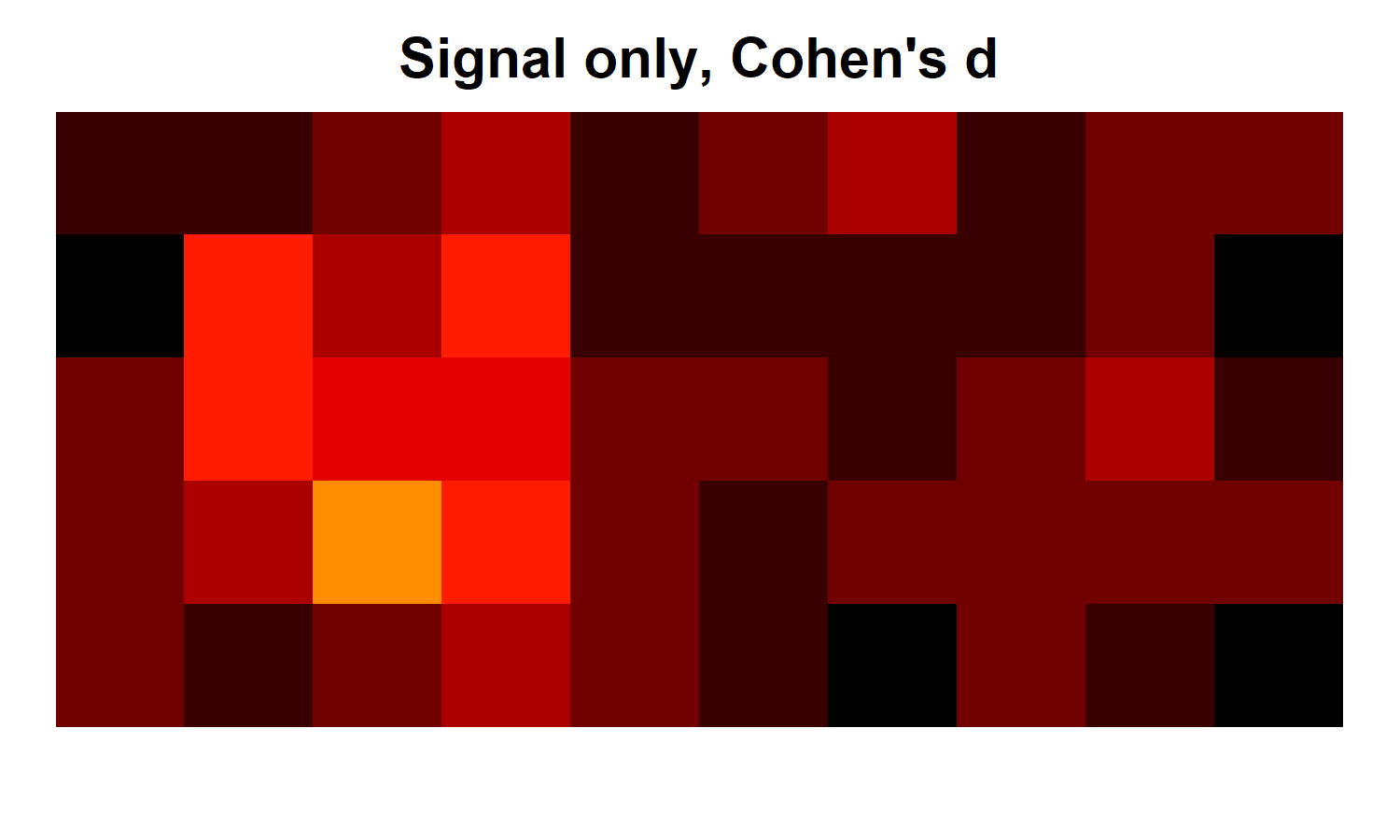
We'll start by simulating a set of 20 5x10 "brains". You can think of these as the 1st level contrasts from 20 participants. Each map will begin as a set of independent random normal N(0,1) numbers. Into this noise, we will insert signal, by adding 1 to each value within a 3x3 region on the left of each brain. You can see the signal amongst the noise in the heatmap below, which visualizes the Cohen's d across participants at each simulated voxel.

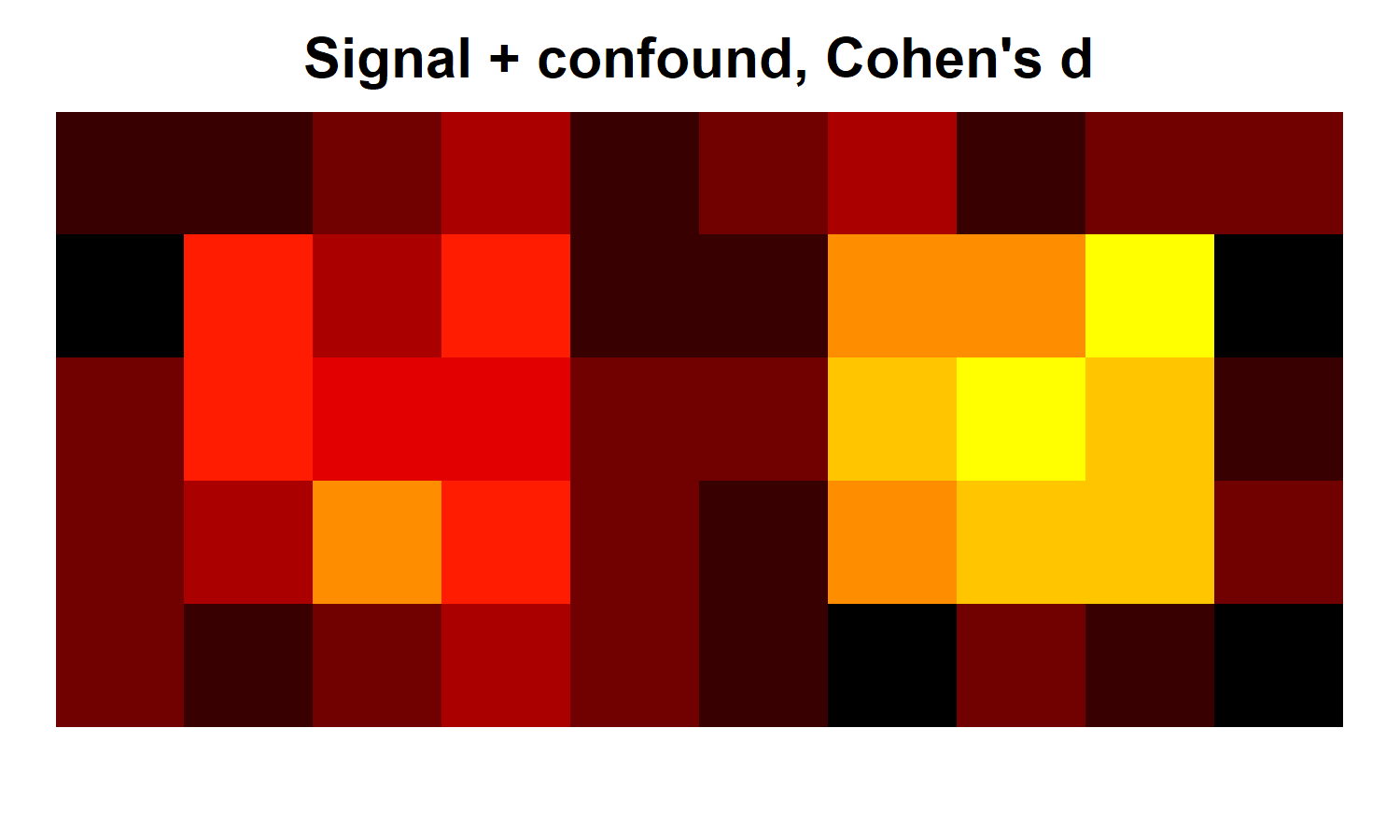
We will also create a second version of these brains, with all of the same noise and signal. However, in this case, we will create a second signal by adding 2 to another 3x3 region on the right side of the brain. This second regions represents a major confound in our "experiment". You can see the Cohen's d for the brains including the confound below.

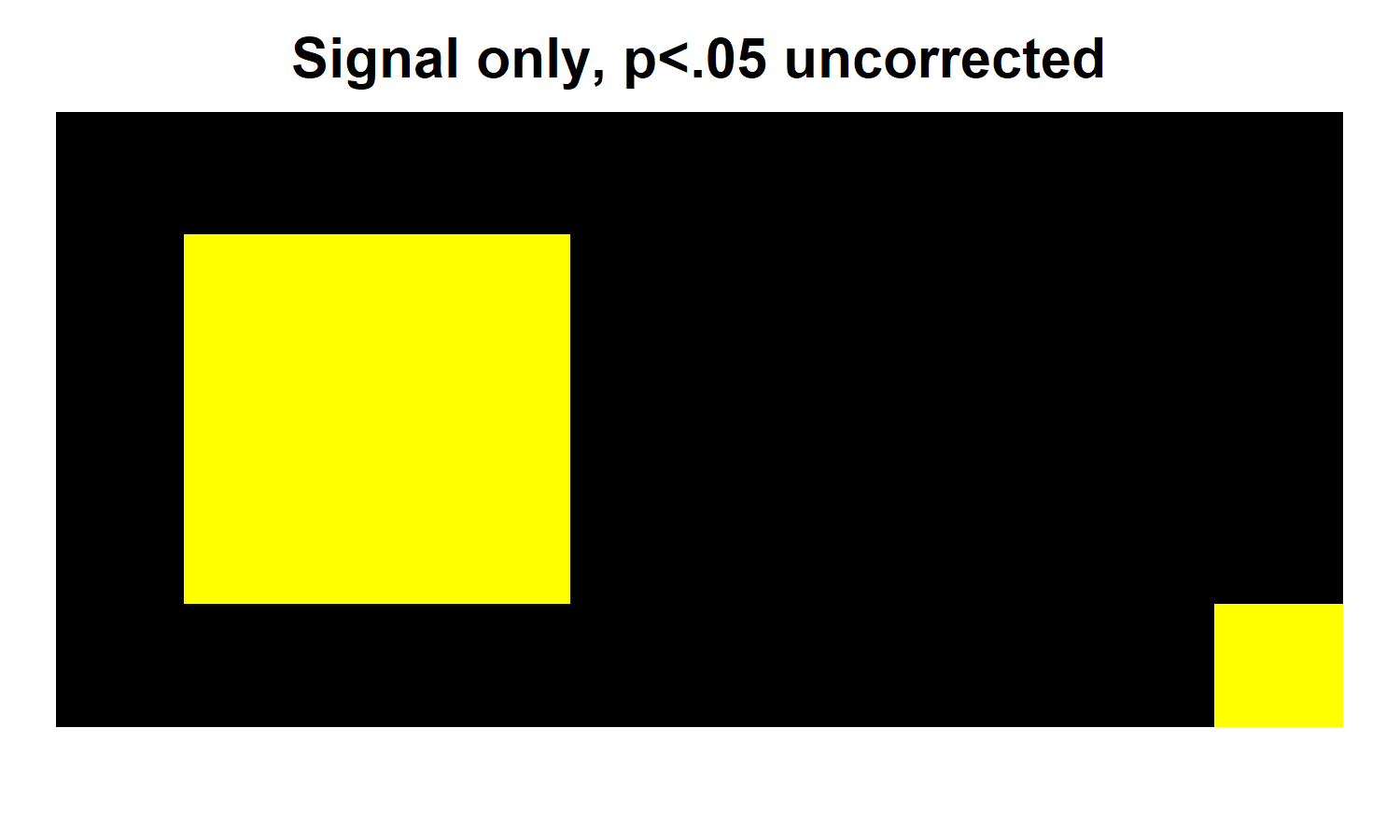
Next, we will apply significance testing to our simulated data. We'll start with the unconfounded (signal only) version of the experiment. The heatmap below shows the voxels that are significant in uncorrected voxelwise one-sample t-tests across participants. As you can see, with this liberal threshold, we easily recover significant (yellow) results in all 9 voxels within our signal region. This is unsurprising, given that we specified that the average Cohen's d = 1 in this region, a very large effect. Notably, however, the uncorrected approach fails in the expected wayby producing a false positive in the lower right of the brain.

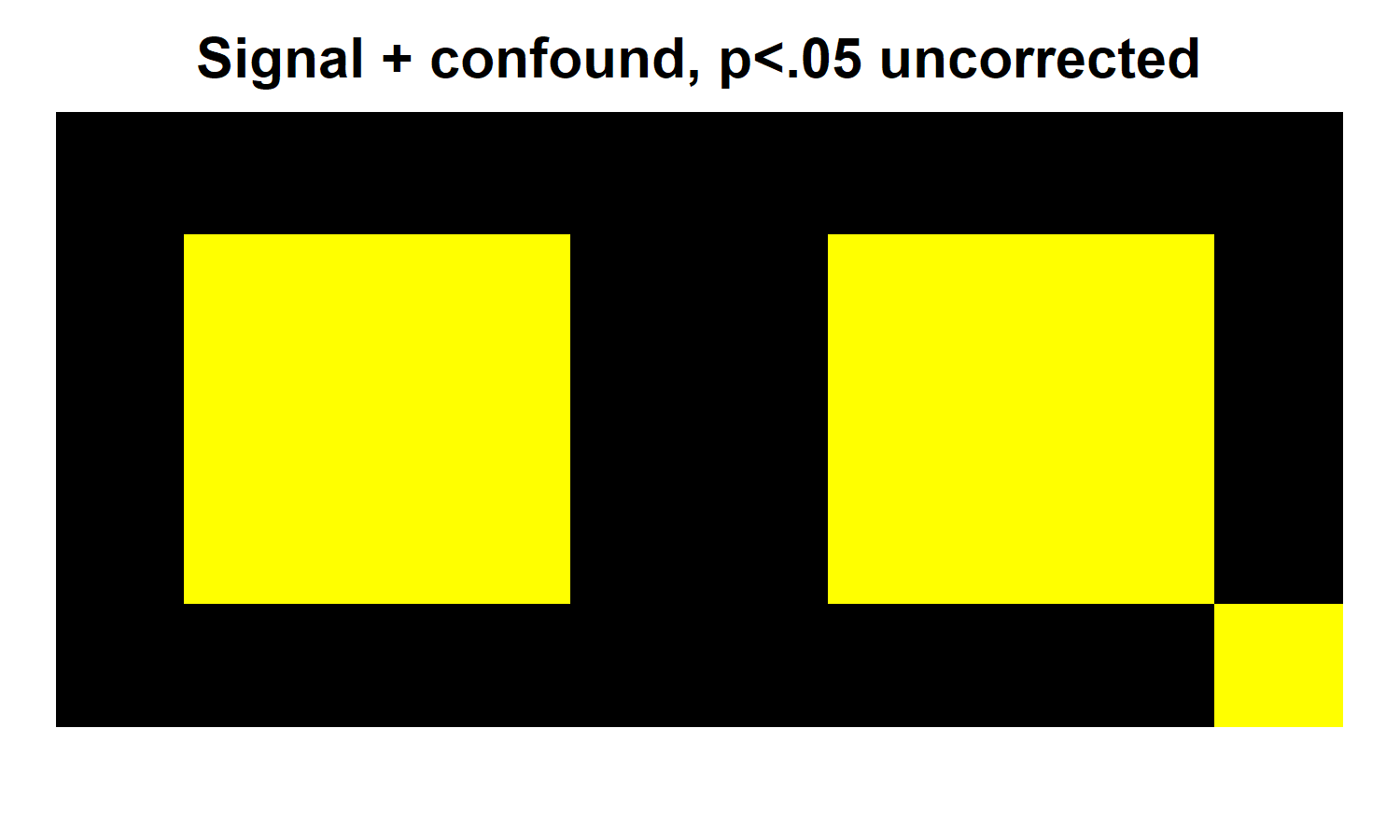
Now we will repeat this procedure in our confounded version of the experiment. You can see the results below. We now also observe significant results in all of the confound region on the right. However, significance in other voxels remains unchanged.

Using uncorrected tests is clearly problematic, since doing so leads to false positives. So let's now correct our results. In this case we'll use the Bonferroni procedure, which sets the corrected significance threshold to alpha/(# of voxels). In this case that works out to p = .05/50 = .001. In realistic analyses, the Bonferroni correction is far from the best way to achieve FWE control, but it works just fine here for illustrative purposes. In the heatmaps below, you can see the results for both the unconfounded and confounded versions of our data.

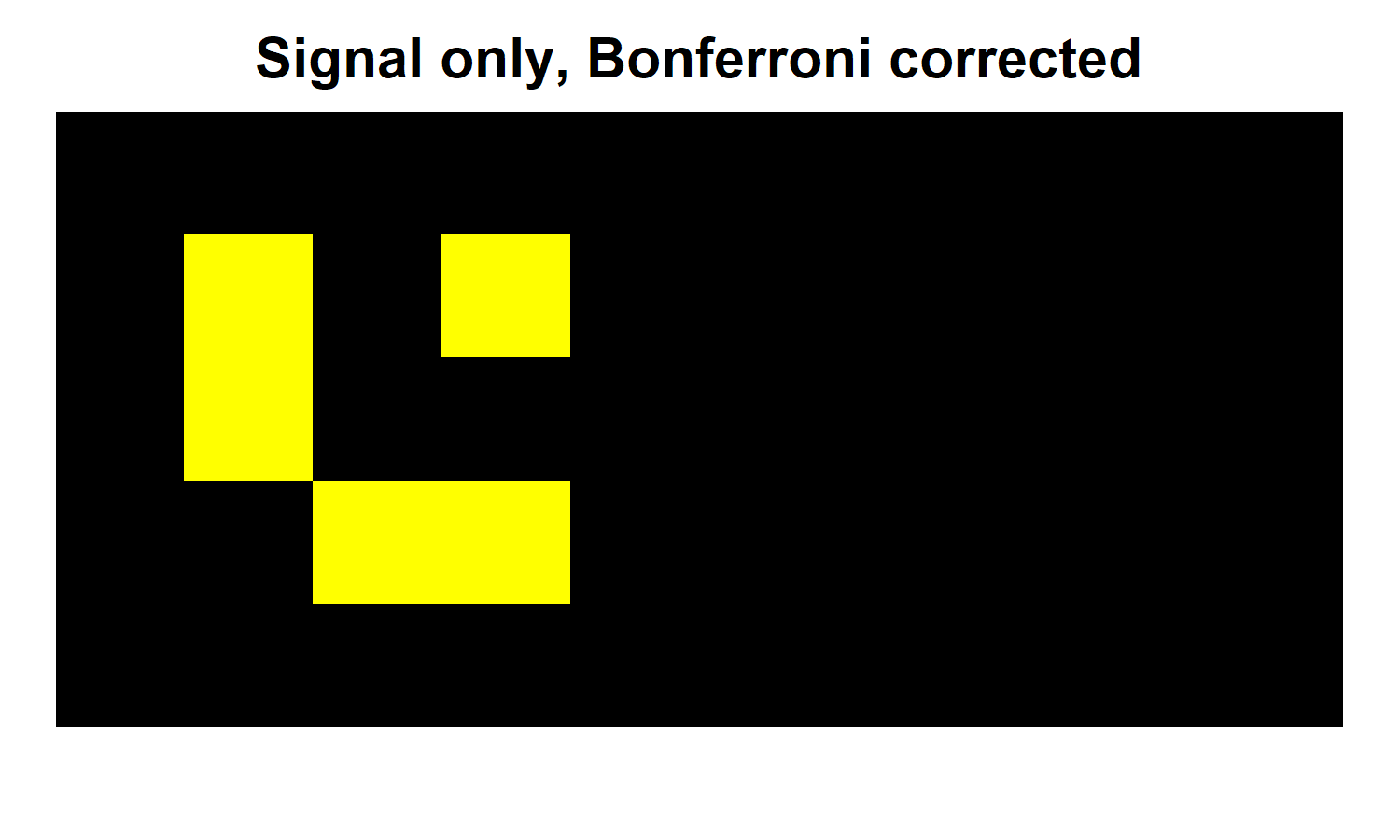
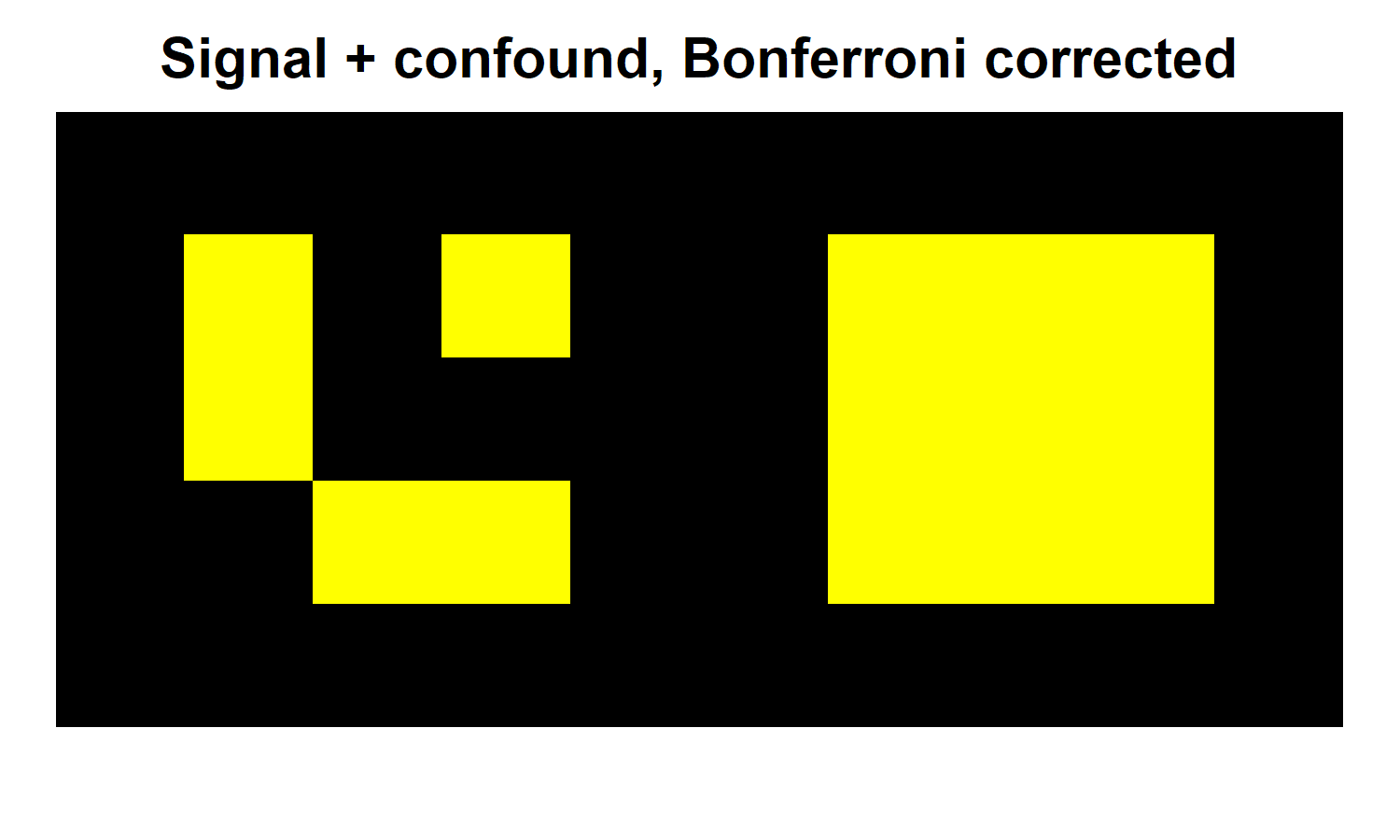
As we should hope, the Bonferroni correction eliminates the false positive in the lower right hand corner. However, it also eliminates 4/9 voxels in our signal region (now false negatives). Importantly, this is the same across both versions of the data, regardless of confound. In the confound region, all voxels remain significant because the effect size in this region is 2X that in the signal region.

Since the Bonferroni correction has arguably gone too far - eliminating half of our true positives to expunge a single false positive - this seems like it might be a good time to try FDR, right? The heatmap below shows the results of correcting for FDR instead of FWE with the unconfounded version of our data.

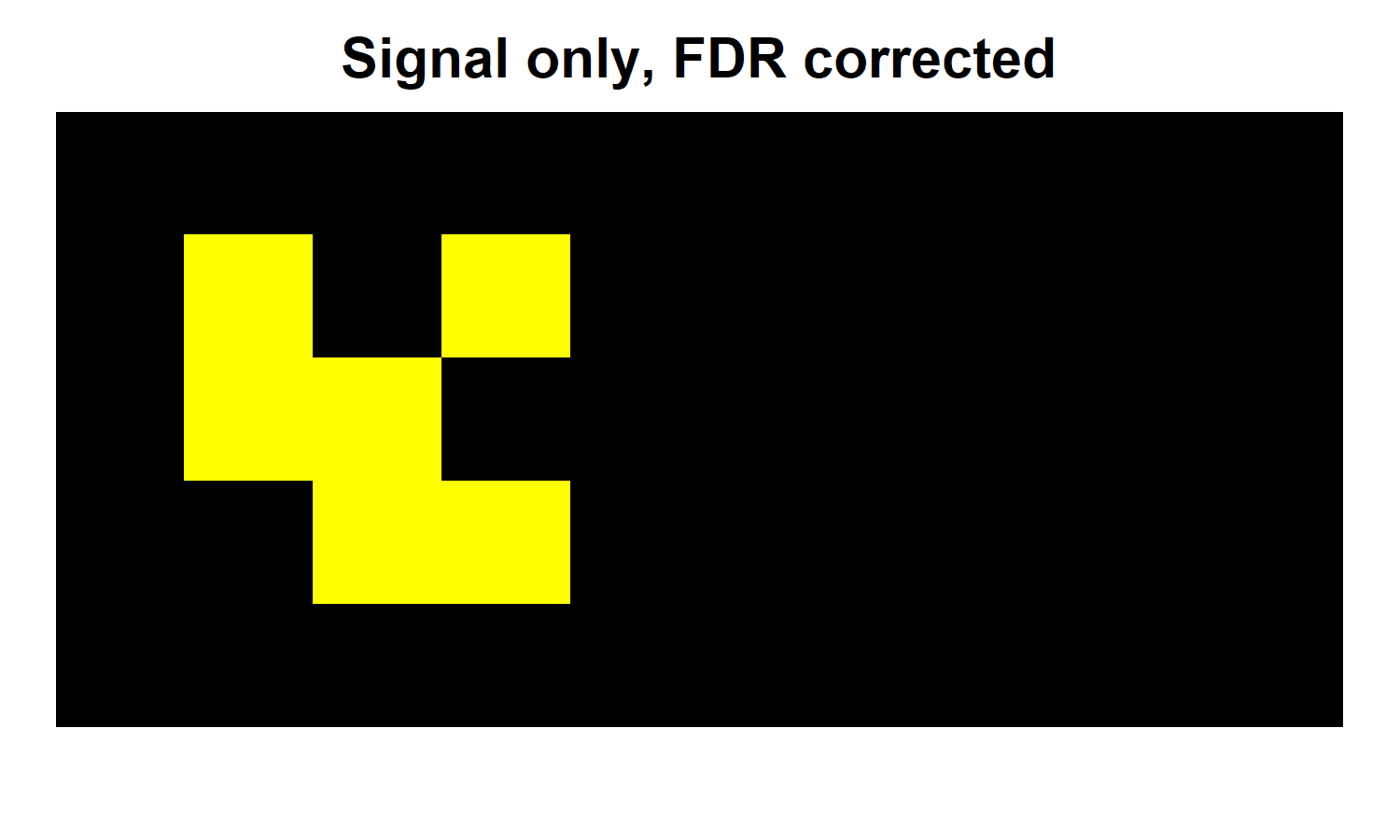
The result above suggests that the FDR correction has worked, at least a bit. It has brought back 1 voxel within our signal region, while still keeping out the false positive in the lower right. Great, right? But what happens when we do the same thing to our confounded data? The heatmap below relates this final result.

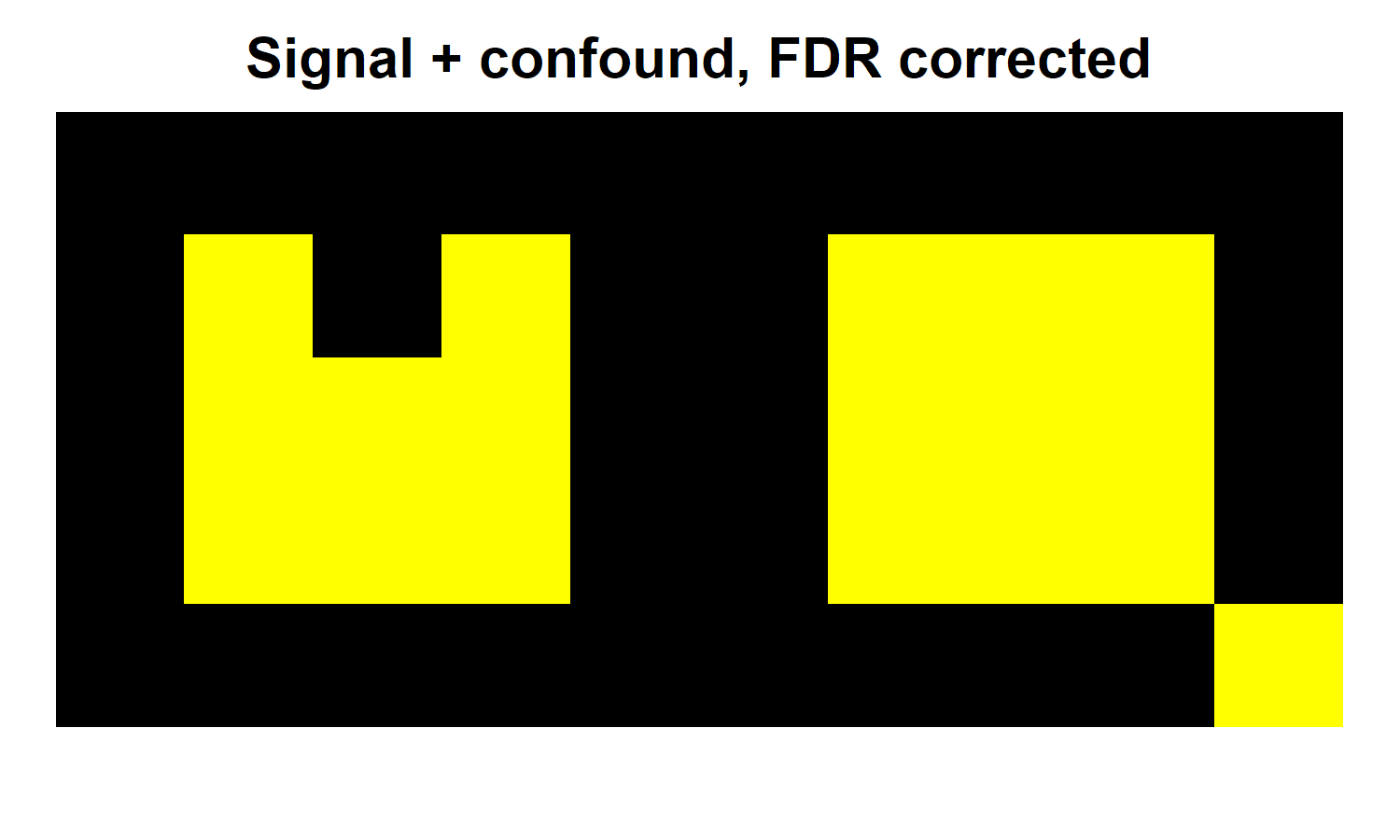
Under the FDR correction, the confound region remains entirely significant, as it did in the Bonferroni case. However, the confound has wrought other changes, outside of the confound region itself. By introducing more true positives, the confound has lowered the bar for other true and false positives alike. As a result, it has permitted the reemergence of our false positive in the lower right.

Unlike with the Bonferroni correction, the presence of the confound region also has consequences for the signal region. Specifically, we see another two true positive reappear here. At first glance, the confound has led us to rediscover more true positives. However, recall that we only know which positives are true or false here because we created the data. In a realistic context, this same phenomenon might lead to more false positives instead.

You can view the Rcode behind these simulations here.

Conclusions

As the simulation above shows, confounds can increase the likelihood of finding significant results when using an FDR correction. This creates a perverse situation in which a confounded study is more likely to turn up significant results (even outside of regions directly related to the confound) and is consequently more likely to get published. In principle, it is possible that one could even intentionally design a study with a major confound in order to capitalize on the lower bar it sets in other regions of the brain. I doubt this happens much, if at all. Even if someone had sufficiently dubious morals to consider it, it would be a risky strategy, since an obvious confound might lead to rejection, independent of the results. However, intentional bad actors are not necessary for systemic problems to emerge: even a slight bias towards confounded papers as a result of FDR could add up to inflict serious damage on the neuroimaging literature over time.

FDR's adaptability also has the potential to cause other biases in the literature. For example, even in the absence of any confounds, FDR will be more permissive when there are large swathes of the brain activated by a manipulation, rather than one or two focal regions. This could bias the modularity-vs-distributed processing debate, as papers finding evidence for distributed networks (with lots of voxels) face a lower bar to significance - and hence publication - than isolated modules.

More broadly, FDR's use is not limited to brain imaging. It is a popular approach in many situations where major multiple comparison problems pop up. Genome-wide association studies (GWAS) in genetics are another example of such a research context. FDR could prove just as problematic in this context, leading to spurious genetic associations and promoting confounded individual difference measures.

For these reasons, I am disinclined to use FDR to mitigate multiple comparisons. Controlling FWE - although admittedly more conservative - produces much more intuitive results than FDR, in my opinion. Moreover, we ar not limited to draconian old corrections like Bonferroni. Most modern FWE corrections take advantage of the high degree of spatial dependency in brain images to achieve far greater power than corrections that assume voxels are independent. For example, maximal statistic permutation testing - particularly in combination with a cluster extent threshold or threshold free cluster enhancement - produce results that are worlds better than Bonferroni, while still retaining FWE control. As time has passed, I've found myself doing less and less whole brain mapping anyway, but when I do, these are the tools that I turn to manage multiple comparisons.

However, there is at least one circumstance in which FDR correction is unlikely to prove problematic: registered reports. As you may have noticed, the mechanism by which FDR promotes confounds is publication bias. Scientific studies with null results are generally harder to publish than those with significant results, and I suspect that this is particularly in the case of fMRI research. Fixing publication bias across the whole field would mean that FDR would no longer perversely reward confounds. However, eliminating this bias from the entire field is not a trivial challenge. Fortunately, many journals now feature a registered report format that guarantees the publication of methodologically sound papers regardless of their result. If one loves the balance between false positive and false negatives that FDR provides, then I would suggest using this correction in context of registered reports, where it cannot favor the publication of confounded studies.