Postings on science, wine, and the mind, among other things.
How Long to Wait for a Date?
Reverse-engineering beliefs about the distribution of response times in online dating using Bayesian modelling
![By PanierAvide (Own work) [CC BY-SA 4.0 (http://creativecommons.org/licenses/by-sa/4.0)], via Wikimedia Commons](../../images/waiting.png)
If you're currently single, or you have been recently, then you've probably tried online dating. Over the past decade online dating has overcome stigma to become the modal solution to the "problem" of being single. A huge number of online dating services have flourished in response, many of them based around mobile apps rather than traditional websites. There has been much hand-wringing over the many novel difficulties of online dating, but here I will focus on one notoriously frustrating aspect: the waiting game.
The vast majority of online dating relies on asynchronous communication: the parties generally do not speak to each other "live" unless and until they decide to meet in person. Thus an exchange will typically begin with one person composing and sending a message to another person. At some point later, the target of this communiqué may read it. The recipient then has to option to respond (whenever suits them) or not.
Many messages never receive a response. Indeed, declining to respond has become a typical method of rejection. Critics have oft bemoaned the transition from explicit rejection to non-response, though there are some practical arguments in favor of it: it spares both parties the pain of explicit rejection; it saves time when dealing with a flood of messages; and it helps avoid boors who won't take "no" for an answer.
Unfortunately, the practice of declining by non-response has created a novel kind of torture for those who send messages in good faith. Senders must wait indefinitely for a response that may never come, a process that can prove agonizing. Indeed, even when they do eventually get a response, senders may wait longer then they need to because recipients delay their responses to avoid appearing too eager or available.
Knowing when to give up hope has thus become one of the most important tools of the modern online dater. Hard data on when this point actually comes is difficult to find. Understandably, online dating services are loath to share such information. Fortunately, we may be able capitalize on some statistical tricks and features of the human mind to infer how long people typically wait to hear back from a prospective date.
Discover the shape of your beliefs:
The methods are described in detail below, but first give it a shot yourself. If you fill out the form below, it will automatically estimate what you believe about the distribution of response times in online dating. Your results will then be visualized in comparison with others like you who have submitted their responses.
Methods
So how does this work? The basic insight is that as we wait for a response from our potential date, we're actually learning something. This may seem counterintuitive: the waiting process can certainly feel like an information vacuum. However, that may be because of the blinding obviousness of what we're learning. Every moment that passes while we wait for a response, we learn this: our (maybe) date will not respond earlier than the present moment. If we've waited 2 hours, the probability of them replying 1 hour after we sent our message is precisely zero. The reason, of course, is that this time has already passed, and responding an hour into the past would require some rather dicey violations of causality.
This information may seem fairly empty, but this type of data guides our decision to eventually give up on receiving a response. The reason is that we have - buried in our minds - some prior beliefs about the likely distribution of response times (as well as the overall response rate). In fact, it turns out people generally have quite accurate prior beliefs about many things with which they have experience, such as how long it generally takes to bake a cake or how long an elected representative can expect to remain in Congress. Moreover, when people learn new information, they generally seem to be able to optimally update their beliefs using Bayes' theorem. It's not yet clear how this process is implemented by neurons in the brain - it certainly isn't conscious in most cases, since most people don't know Bayes theorem explicitly.
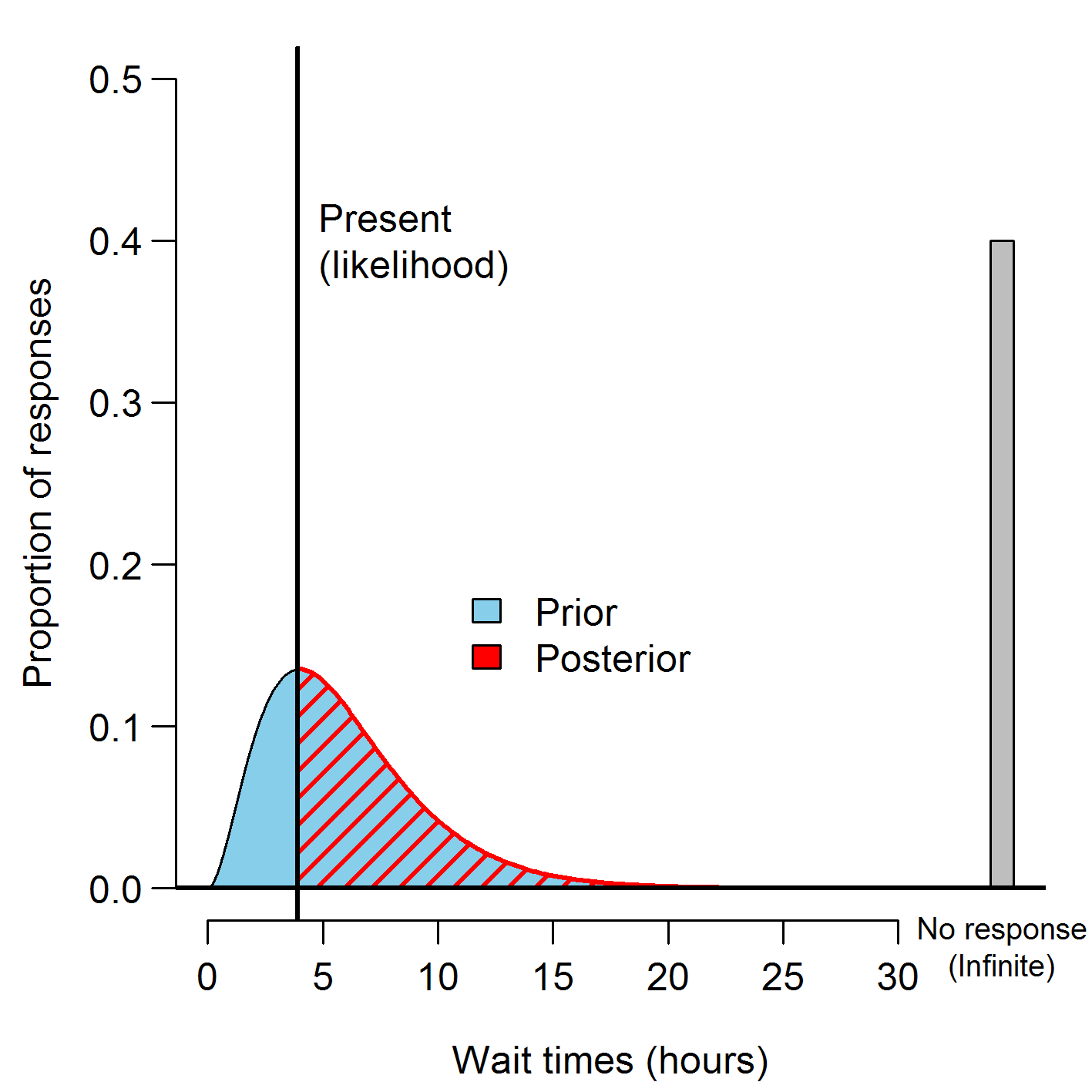
In the present case, combining the information we learn by waiting with our (hopefully accurate) prior beliefs about response times produces a very simple change in our belief, illustrated above. At any given moment, we combine our general belief about the distribution of weight times (prior) with new information provided by how long we've waited so far (likelihood) to produce an updated belief (posterior) about the distribution of (remaining possible) wait times. In this very simple case, the prior simply gets zeroed out as the present advances.
Now think back to the form you filled out above. We asked you to estimate your chance of eventually getting a response, given that a certain amount of time had passed. To figure this out, your mind implicitly compared the area under the curve in the red region (remaining wait times for an actual response) with the area in the grey bar (proportion of messages which never receive a response). The longer the wait, the smaller the region under the red curve compared to the grey region, and so the greater the chance that a message will go permanently unanswered. This makes sense intuitively: if we've waited weeks for a response, we should know we're not likely to get one.
In mathematical terms, the estimates you provided above roughly correspond to points on a curve known as a cumulative distribution function (CDF) for your beliefs about the distribution of wait times. Conveniently, by taking the derivative of a CDF we can transform it into a probability density function (such as those in graphs above). As simply as that, we have a good estimate for how long people have to wait for a date!
Conclusion
As I'm writing this post before any results come in, I don't yet have any interpretation to add to the aggregate data you can see above. If and when enough responses accumulate, I may add something more here or post a follow-up blog in which I slice up the data on the basis of dating service. I'll end by acknowledging my debt to Tom Griffiths and Josh Tenenbaum - this post is merely a fun derivate of their research on everyday Bayesian cognition. I was reminded of their work and inspired to do something with it while reading Tom's recent book (with Brian Christian) - Algorithms to Live By - which I highly recommend.
© 2016 Mark Allen Thornton. All rights reserved.
